Description on Maxwell equations
Published:
Maxwell’s equations
Maxwell’s equations are set of coupled partial differential equations, that combines all of the phenomena discovered by Oersted, Ampère, Henry, Faraday and others into set of 4 equations which then became the foundation of classical electromagnetism, optics, magnetism and electricity. The equations acts as mathematical model for electrical, radio, electric motors, sensors, radar and lenses etc.
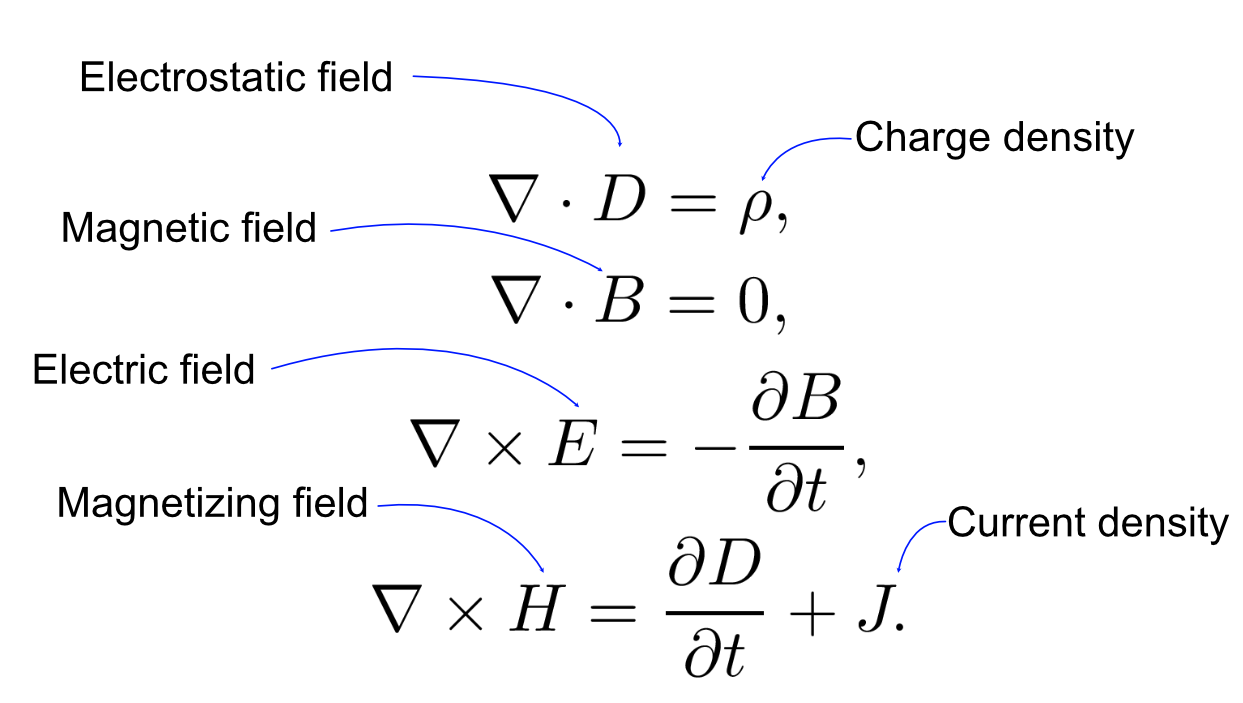
Maxwell’s First Equation
Maxwell’s first equation is derived from Gauss’s theorem which states, the surface integral of the electrostatic field D over a closed surface is equal to the charge enclosed by that surface.
\[\int_{\text {surface }} \mathbf{D} \cdot d \boldsymbol{\sigma}=\int_{\text {volume }} \rho d v\]Here ρ is the charge per unit volume, \(\boldsymbol{\sigma}\) is the area vector.
Since, surface integral of a vector field over a closed surface is equal to the volume integral of it’s divergence, and therefore
\[\int_{\text {volume }} \operatorname{div} \mathbf{D} d v=\int_{\text {volume }} \rho d v\]which gives
\[\nabla \cdot D=\rho\]Maxwell’s Second Equation
Magnetic lines of force are closed curves and the magnetic fields have no source or sinks. Consequently the surface integral of the magnetic field over a closed surface is zero and therefore
\[\int_{\text {surface }} \mathbf{B} \cdot d \boldsymbol{\sigma}= \int_{\text {volume }} \operatorname{div} \mathbf{B} d v = 0\]which gives
\[\nabla \cdot \mathbf{B} = 0\]Electric field has source and sink
Maxwell’s Third Equation
Based on the Faraday’s and Len’z laws of electromagnetic induction, which state that the \(e.m.f.\) induced in a closed circuit is equal to minus the rate of change of B-flux through the circuit i.e. surface integral of \(\mathbf {\dot B}\)
\[e.m.f. = - \int_{\text {surface }} \operatorname{curl} \mathbf {\dot B} . d \boldsymbol{ \sigma}\]Since \(e.m.f.\) around a closed circuit is the line integral of electric field \(E\) around the circuit , which is equal to the surface integral of it’s curl, as defined below
\[e.m.f = \int_{\text {line }} \mathbf{E} \cdot d \boldsymbol{s}= \int_{\text {surface }} \operatorname{curl} \mathbf{E}. d \boldsymbol{ \sigma}\]Therefore,
\[\int_{\text {surface }} \operatorname{curl} \mathbf{E}. d \boldsymbol{ \sigma} = - \int_{\text {surface }} \operatorname{curl} \mathbf {\dot B} . d \boldsymbol{ \sigma}\]which gives,
\[\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}\]Maxwell’s Fourth Equation
This law is derived from Ampere theorem, which state that the line integral of the magnetic field H around a closed circuit is equal to the enclosed current.
\[\int_{\text {loop }} \mathbf{H} \cdot \mathbf{d s}=\int_{\text {area }}(\dot{\mathbf{D}}+\mathbf{J}) \cdot \mathbf{d} \sigma\]Since, he line integral of a vector field around a closed plane curve is equal to the surface integral of its curl, therefore
\[\int_{\text {area }} \operatorname{curl} \mathbf{H} \cdot d \sigma=\int_{\text {area }}(\dot{\mathbf{D}}+\mathbf{J}) \cdot \mathbf{d} \sigma\]which gives
\[\operatorname{curl} \mathbf{H}=\dot{\mathbf{D}}+\mathbf{J}\]or
\[\nabla \times \mathbf{H} =\frac{\partial \mathbf{D}}{\partial t}+ \mathbf{J}\]Reference - Physics LibreTexts
